
We previously saw how the Bulletproofs Inner Product Argument (IPA) works: it lets us prove that we know a secret vector without revealing it.
That’s neat, but what can we actually do with it?
→ Range proofs!
Bulletproofs are the backbone of modern range proofs: they allow us to prove that a secret value lies within a given range, without revealing the value itself.
Don’t worry if you haven’t read the previous IPA articles, you can think of the IPA as a black box that proves an inner product relation without exposing the vectors. Though… if you do want to understand it, go read Breaking Down Bulletproofs (part 1) and Unfolding the Bulletproofs Magic (part 2).
Here’s a quick overview of what we’ll go through today 😅
(this diagram comes from the excellent Dalek Bulletproofs documentation)
Nooo! 🥲 Don’t stop here! I promise that by the end of this article, this strange-looking graph will make perfect sense.
A motivating example
A great use case is confidential transfers.
Imagine you want to send money to a friend, but you don’t want anyone else to see how much. You still need to prove that the transfer makes sense: you’re not sending a negative amount or exceeding your balance.
In many privacy-preserving systems (for example, when balances are represented by homomorphic commitments), this requires proving that both the amount and the resulting balance stay within valid ranges, preventing overflows/underflows, without revealing their actual values.
For instance:
- the maximum amount you can transfer is 100
- the maximum balance allowed is 1000
You would produce two range proofs:
-
Transfer amount is valid: 0 ≤ amount ≤ 100
-
Resulting balance is valid: 0 ≤ balance - amount ≤ 1000
If both hold, your transfer is correct… without revealing the actual numbers.
These kinds of proofs are called range proofs, and Bulletproofs are one way to build them efficiently.
Other constructions exist too (see, for instance, the 2024 SoK paper), but Bulletproofs remain among the most practical today. They were famously adopted by Monero to enable confidential transactions in production.
What are we trying to prove?
We want to prove that a secret value $v$ lies in the range $[0,2^n)$, without revealing $v$.
You can adapt the same logic to any range $[a,b]$, but today I’ll keep powers of 2, it makes the math cleaner.
As you probably guessed, we’ll reuse our vector machinery and the Inner Product Argument we built earlier (need a refresher? checkout out Breaking Down Bulletproofs (part 1) and Unfolding the Bulletproofs Magic (part 2) 😁).
Notations
Whenever I use bold, it means I’m talking about a vector.
- $\mathbf{2}^n = (2^0,2^1,2^2,...,2^{n-1})$
vector of length n of successive powers of 2
- $\mathbf{0}^n = (0,0,...,0)$
vector of n zeros
- $\mathbf{1}^n = (1,1,...,1)$
vector of n ones
- $\mathbf{y}^n = (y^0,y^1,y^2,...,y^{n-1})$
vector of length n of successive powers of a random value y
- $z\mathbf{1}^n = (z,z,...,z)$
vector n elements, all equal to z ($\mathbf{1}^n$ scaled by $z$)
Breaking our secret number into bits
The key trick in Bulletproofs range proofs is bit decomposition, breaking a secret number into its individual bits.
This is the same basic approach used in other systems as well: you prove that each bit is either 0 or 1, and that their weighted sum reconstructs the value. In Circom, for example, this is done with the Num2Bits gadget.
Although newer proving systems sometimes use lookup-based range checks for efficiency, bit decomposition remains the fundamental building block that most protocols rely on.
We represent the secret value $v$ as a sum of its bits.
Let $\mathbf{a}_L$ be the vector of bits of $v$.
For example, if $v = 123 = 0b1111011$:
$$ \mathbf{a}_L = (1,1,1,1,0,1,1) $$Then:
$$ \langle \mathbf{a}_L,\mathbf{2}^n \rangle=v $$That inner product expresses exactly how binary numbers work:
$$ a_{L_0} \cdot 2^0 + a_{L_1} \cdot 2^1 + ... + a_{L_{n-1}} \cdot 2^{n-1} = v $$(note: here i’m assuming that $\mathbf{a}_L$ is in little endian)
With our example (in big-endian form):
$$ \begin{aligned} &1 \cdot 2^6 + 1 \cdot 2^5 + 1 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 \\ =& \text{ } 64 + 32 + 16 + 8 + 2 + 1 \\ =& 123 \end{aligned} $$Our range proof will revolve around convincing the verifier that:
- this equation holds, and
- each $\mathbf{a}_{L_i}$ really is a bit (0 or 1)
That’s important because the verifier will only ever see a commitment to $\mathbf{a}_L$, not the vector itself. So without this check, the prover could hide arbitrary values inside the commitment and still make the equations balance.
Convincing the verifier our bits are real 0s and 1s
We can’t just tell the verifier our bits, that would reveal $v$.
So we need a way to prove that every component of $\mathbf{a}_L$ is either 0 or 1.
For a single number $x$, being a bit means:
$$ x \cdot (x-1)=0 $$Only if $x$ is 0 or 1 does the equation hold.
For vectors, we use element-wise (Hadamard) multiplication $\circ$:
$$ \mathbf{x} \circ (\mathbf{x}-\mathbf{1}^n) = \mathbf{0}^n $$So we define a new vector:
$$ \mathbf{a}_R = \mathbf{a}_L - \mathbf{1}^n $$and we want to prove that:
$$ \mathbf{a}_L \circ \mathbf{a}_R = \mathbf{0}^n $$which ensures that all entries of $\mathbf{a}_L$ are binary.
You might wonder why we introduce a new vector instead of just using $\mathbf{a}_L - \mathbf{1}^n$ directly in the equation.
The reason is mostly structural: we need to refer to both $\mathbf{a}_L$ and $\mathbf{a}_R$ in different parts of the proof, sometimes together and sometimes separately.
By assigning this expression to its own variable, we make later equations cleaner and easier to work with, especially when we start building inner products and commitments involving each vector independently. Each vector plays a different role in the proof, and defining them explicitly ensures those commitments remain consistent with the constraints we’re enforcing.
You can also think of it as a circuit, where each operation produces a new variable and we constrain each relation.
In pseudocode, that would look like:
def range_proof_circuit(params, priv, pub):
bitlen = params
com_v = pub
a_L, a_R, ... = priv
assert com(sum(a_L * power_of_2)) == com_v
assert a_R == a_L - vec_1
assert a_L * a_R == vec_0
A clever probabilistic trick
How can we prove that two hidden vectors multiply to zero without revealing them?
We start with a simple intuition: suppose you want to prove that a secret number $x$ equals 0.
If the verifier gives you a random value $r$, and you respond with
$$ x \cdot r = 0 $$(we suppose you can’t cheat, and have to send the actual result of that product)
then unless you’re (really) lucky, the only way that can hold is if $x=0$.
We apply the same idea to vectors, but there’s a subtle difference…
Schwartz–Zippel for inner-product
We just saw how a random challenge can help check that a single value equals zero.
Here, we actually have several equations (one per vector element) that we want to hold simultaneously:
$$ a_i \cdot b_i = 0 \quad \forall i $$If this isn’t the case, the terms could cancel each other out.
For example, with a vector of length 3, you could have:
$$ \begin{aligned} a_0 \cdot b_0 &= 6 \\ a_1 \cdot b_1 &= -4 \\ a_2 \cdot b_2 &= -2 \\ \end{aligned} $$Even though each row is nonzero, their sum (the inner product) equals 0, which is not what we want.
To avoid that, we add randomness to each row.
This way, even if you try to cheat, you can’t predict how to make the terms cancel.
The verifier sends a random vector $\mathbf{r}$ of length $n$, and the prover must now show:
$$ \langle \mathbf{a}_L \circ \mathbf{a}_R, \mathbf{r} \rangle = 0 $$Why does this work?
Because the random coefficients in $\mathbf{r}$ act as independent scalings for each term, so any potential cancellations become essentially impossible.
If this equality holds for a random challenge $\mathbf{r}$, it’s overwhelmingly likely that the element-wise products themselves are all zero.
Formally, this relies on the Schwartz–Zippel lemma: we treat the left-hand side as a polynomial and test whether it evaluates to zero at a random point. If it does, it’s very likely that the whole polynomial is identically zero, and the probability of being fooled is at most $\frac{d}{|\mathbb{F}|}$.
To reduce communication, the verifier doesn’t send the whole vector $\mathbf{r}$, but just a single random value $y$.
The prover then constructs $\mathbf{r}=\mathbf{y}^n=(1,y,y^2,...,y^{n-1})$
$a_R$ is correctly formed
We have one last issue… we also need to show that $\mathbf{a}_R$ was defined honestly:
$$ \mathbf{a}_R \stackrel{?}{=} \mathbf{a}_L - \mathbf{1}^n $$Easy! We do this by proving another inner product equals zero:
$$ \langle \mathbf{a}_L - \mathbf{1}^n - \mathbf{a}_R , \mathbf{y}^n \rangle = 0 $$Again, because the verifier choses $y$ randomly, the prover can’t fake it.
Recap: everything we must prove
In summary, the prover needs to prove three relations, each reduced to an inner product that can be verified using the IPA:
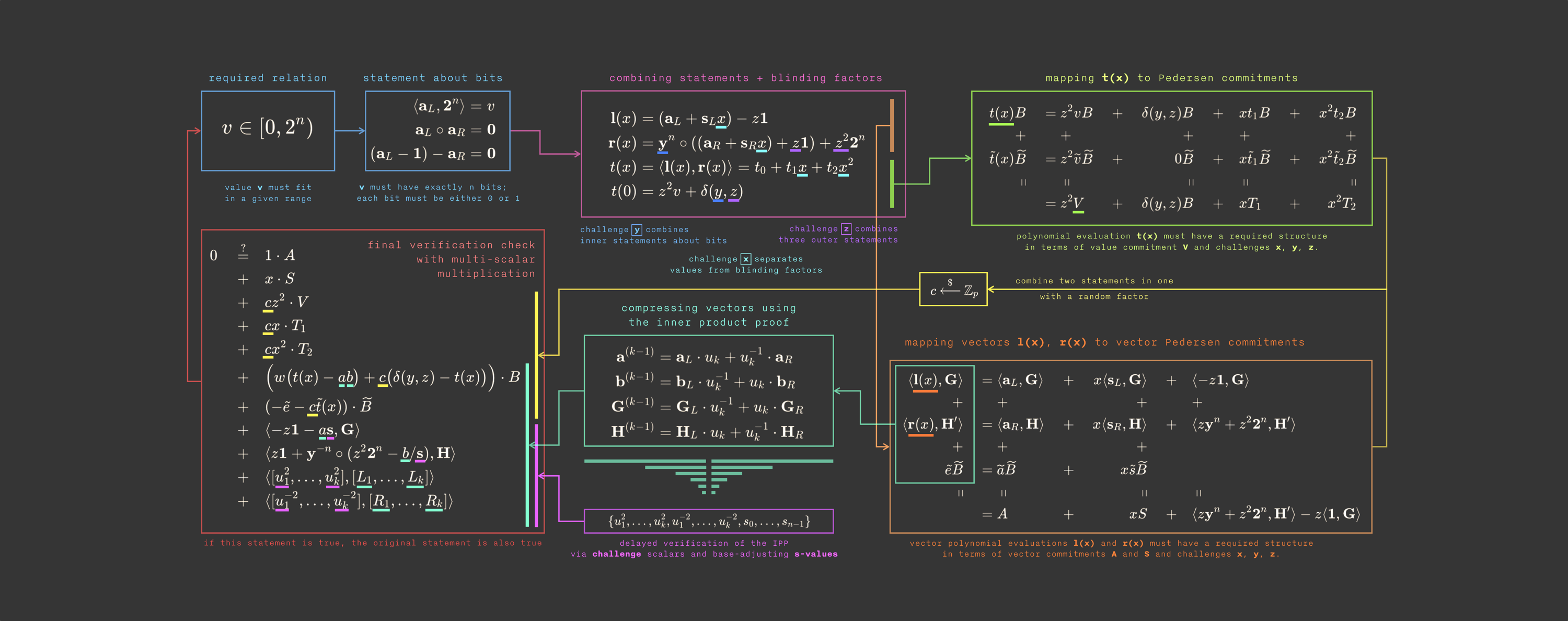
$$ \begin{aligned} \langle \mathbf{a}_L , \mathbf{2}^n \rangle &= v \\ \langle \mathbf{a}_L - \mathbf{1}^n - \mathbf{a}_R , \mathbf{y}^n \rangle &= 0 \\ \langle \mathbf{a}_L, \mathbf{a}_R \circ \mathbf{y}^n \rangle &= 0 \end{aligned} $$Notice that I slightly rearranged the third equation.
It’s equivalent to what we had before:
$$ \langle \mathbf{a}_L \circ \mathbf{a}_R, \mathbf{y}^n \rangle = 0 $$but the structure of the equation now aligns better with how Bulletproofs commitments are expressed later on.
That’s our full setup! From here, we’ll move on to the heavier algebra that ties everything together.
Combining inner products
So far, we have three separate inner products to prove.
That’s quite a bit to handle.
Ideally, we’d like to bundle them into one single inner product that can be proven with a single IPA.
To do that, we introduce another random challenge from the verifier: $z$.
Then we take a random linear combination of the three equations using powers of $z$:
$$ \begin{aligned} &z^2 \cdot \langle \mathbf{a}_L, \mathbf{2}^n \rangle + \\ &z \cdot \langle \mathbf{a}_L - \mathbf{1}^n - \mathbf{a}_R, \mathbf{y}^n \rangle + \\ &\langle \mathbf{a}_L, \mathbf{a}_R \circ \mathbf{y}^n \rangle\\ &= z^2 \cdot v \end{aligned} $$That way, the prover can’t “tune” each equation independently to cheat. Everything must be consistent across the combination.
We now want to rearrange this equation so that:
- the left part of the inner product is only a function of $\mathbf{a}_L$
- the right part depends only on $\mathbf{a}_R$
- the result depends only on $v$, and constants known to the verifier
That clean separation will make it much easier to later commit to each side independently.
First expand:
$$ z^2 \cdot {\langle \mathbf{a}_L, \mathbf{2}^n \rangle} + z \cdot {\langle \mathbf{a}_L,\mathbf{y}^n \rangle} - z \cdot {\langle \mathbf{a}_R,\mathbf{y}^n \rangle} - z \cdot {\langle \mathbf{1}^n,\mathbf{y}^n \rangle} + {\langle \mathbf{a}_L,\mathbf{a}_R \circ \mathbf{y}^n \rangle} = {z^2 \cdot v} $$Then move $- z \cdot {\langle \mathbf{a}_R,\mathbf{y}^n \rangle}$ to the other side, and move $z$ into the inner products:
$$ \begin{aligned} z^2 \cdot {\langle \mathbf{a}_L, \mathbf{2}^n \rangle} + z \cdot {\langle \mathbf{a}_L, \mathbf{y}^n \rangle} - z \cdot {\langle \mathbf{1}^n, \mathbf{a}_R \circ \mathbf{y}^n \rangle} + {\langle \mathbf{a}_L, \mathbf{a}_R \circ \mathbf{y}^n \rangle} &= {z^2 \cdot v} + z \cdot {\langle \mathbf{1}^n,\mathbf{y}^n \rangle} \\{\langle \mathbf{a}_L, z^2 \cdot \mathbf{2}^n \rangle} + {\langle \mathbf{a}_L, z \cdot \mathbf{y}^n \rangle} + {\langle -z\mathbf{1}^n, \mathbf{a}_R \circ \mathbf{y}^n \rangle} + {\langle \mathbf{a}_L, \mathbf{a}_R \circ \mathbf{y}^n \rangle} &= {z^2 \cdot v} + z \cdot {\langle \mathbf{1}^n,\mathbf{y}^n \rangle} \end{aligned} $$Finally group by $\mathbf{a}_L$ and $\mathbf{a}_R \circ \mathbf{y}^n$
$$ {\langle \mathbf{a}_L, z^2 \cdot \mathbf{2}^n + z \cdot \mathbf{y}^n + \mathbf{a}_R \circ \mathbf{y}^n \rangle} + {\langle -z\mathbf{1}^n, \mathbf{a}_R \circ \mathbf{y}^n \rangle} = {z^2 \cdot v} + z \cdot {\langle \mathbf{1}^n,\mathbf{y}^n \rangle} $$Now add the same term to both sides:
$$ \langle -z\mathbf{1}^n, z^2 \cdot \mathbf{2}^n + z \cdot \mathbf{y}^n \rangle $$After simplifying, we obtain:
$$ \begin{aligned} {\langle \mathbf{a}_L, z^{2} \cdot \mathbf{2}^n + z \cdot \mathbf{y}^n + \mathbf{a}_R \circ \mathbf{y}^n \rangle} + {\langle -z \mathbf{1}^n , z^2 \cdot \mathbf{2}^n + z \cdot \mathbf{y}^n + \mathbf{a}_R \circ \mathbf{y}^n \rangle} &= z^2 \cdot v + z \cdot {\langle \mathbf{1}^n, \mathbf{y}^n \rangle} - {\langle z \mathbf{1}^n, z^2 \cdot \mathbf{2}^n + z \cdot \mathbf{y}^n \rangle} \\ {\langle \mathbf{a}_L - z\mathbf{1}^n, z^{2} \cdot \mathbf{2}^n + z \cdot \mathbf{y}^n + \mathbf{a}_R \circ \mathbf{y}^n \rangle} &= z^2 \cdot v + (z - z^2) \cdot {\langle \mathbf{1}^n, \mathbf{y}^n \rangle} - z^3 \cdot {\langle \mathbf{1}^n, \mathbf{2}^n \rangle} \end{aligned} $$Every term on the right-hand side (except $v$) is known to the verifier, so we can group them into a single known value $\delta(y,z)$, which only depends on the random challenges:
$$ \delta(y,z)=(z-z^2) \cdot \langle \mathbf{1}^n, \mathbf{y}^n \rangle - z^3 \cdot \langle \mathbf{1}^n, \mathbf{2}^n \rangle $$And with that, we finally get the single inner product we’ll work with going forward:
$$ \langle \mathbf{a}_L - z\mathbf{1}^n, \mathbf{y}^n \circ (\mathbf{a}_R + z\mathbf{1}^n) + z^2 \cdot \mathbf{2}^n \rangle = z^2 \cdot v + \delta(y,z) $$We’ve now combined all three constraints into one compact inner product.
The random challenge $z$ ties them together so that the prover can’t selectively satisfy one and not the others.
This equation is the exact form we’ll use in the next step, when we blind and commit to the vectors.
SageMath setup
Before going further, let’s add a bit of code.
From now on, I’ll use short SageMath snippets to illustrate each step of the proof.
We’ll work over a tiny toy field to keep computations simple (real systems use large 256-bit fields).
Specifically, we’ll use:
- the prime field $\mathbb{F}_{929}$,
- the elliptic curve over that field: $y^2=x^3+5x+15$, which has a prime order 919
p = 929
Fp = GF(p)
E = EllipticCurve(Fp, [5, 15])
Fr = GF(E.gens()[0].order())
The goal is to check that $v$ is 8 bits
$$ v \in [0,2^8) $$We define the vectors:
- $\mathbf{1}^n$
- $\mathbf{2}^n$
and then decompose $v$ into bits to form $\mathbf{a}_L$, and $\mathbf{a}_R$
n = 8 # number of bits
print(f"We will be proving that v is between 0 and {pow(2, n)}\n")
# (2^0, 2^1, 2^2, ..., 2^(n-1))
vec_2n = vector([Fr(2 ^ i) for i in range(n)])
# (1, 1, 1, ..., 1)
vec_1n = vector([Fr(1)] * n)
v = Fr(random.randint(0, pow(2, n)))
print("v =", v)
v_bin = bin(v)[2:].zfill(n)[::-1][:n]
print("v_bin = ", v_bin)
aL = vector([Fr(int(bit)) for bit in v_bin])
assert v == sum([aL[i] * 2 ^ i for i in range(n)])
assert v == inner_product(aL, vec_2n)
# Define aR
aR = aL - vec_1n
assert inner_product(aL, aR) == 0
print("aL = ", aL)
print("aR = ", aR)
This matches our earlier equation:
$$ v = \langle \mathbf{a}_L , \mathbf{2}^n \rangle $$The core proof (without zero-knowledge)
If we stopped here, we could already run an Inner Product Argument (IPA) on our combined inner product and get a valid proof, just like in the previous article 😊.
But there’s a problem: the IPA is not hiding. It would reveal information about the witness, possibly leaking the secret value $v$.
In the real protocol, we’ll fix this using blinding vectors $\mathbf{s}_L,\mathbf{s}_R$.
Before getting there, let’s strip things down and see how a simplified version, without any blindings, would work.
We start from the previously combined relation, and name these two sides of the inner product:
$$ \begin{aligned} \mathbf{l} &= \mathbf{a}_L - z\mathbf{1}^n \\ \mathbf{r} &= \mathbf{y}^n \circ (\mathbf{a}_R + z\mathbf{1}^n) + z^2 \cdot \mathbf{2}^n \end{aligned} $$A completely naive protocol would have the prover just send $(\mathbf{l},\mathbf{r})$ and prove that
$$ \langle \mathbf{l},\mathbf{r} \rangle = z^2 \cdot v + \delta(y,z) $$But that’s neither binding nor private. Anyone could fake vectors that satisfy the equation.
So we add commitments.
Commit
At the start of the protocol (before knowing $y,z$), the prover commits to the bit vectors and the value $v$:
$$ \begin{aligned} A &= \langle \mathbf{a}_L, \mathbf{G} \rangle + \langle \mathbf{a}_R, \mathbf{H} \rangle + \alpha \cdot H \\ V &= v \cdot G + \gamma \cdot H \end{aligned} $$Here:
- $\mathbf{G}$ and $\mathbf{H}$ are vectors of elliptic-curve generators (one per bit of $\mathbf{a}_L$)
- $G,H$ are single generators, for scalar commitments
- $\alpha,\gamma$ are random scalars used for hiding (blinding factors)
# Define generators
G = E.random_point()
H = E.random_point()
Gs = [E.random_point() for _ in range(n)]
Hs = [E.random_point() for _ in range(n)]
# Commit to v
print("\nWe can commit to v from the start")
blinding_gamma = Fr.random_element()
V = v * G + blinding_gamma * H
print(f"v commitment (V): {V}\n")
blinding_alpha = Fr.random_element()
A = inner_product(aL, Gs) + inner_product(aR, Hs) + blinding_alpha * H
print("A = ", A)
print("\nProver sends A, V to Verifier")
Then the verifier sends the challenges $y,z$
print("Verifier sends random challenges y and z\n")
y = Fr.random_element()
vec_y_n = vector([y ^ i for i in range(n)])
z = Fr.random_element()
vec_z_1n = vector([z] * n)
So we can now define our main relation $\langle \mathbf{l},\mathbf{r} \rangle = z^2 \cdot v + \delta(y,z)$
l = aL - vec_z_1n
r = aR.pairwise_product(vec_y_n) + vec_y_n * z + z ^ 2 * vec_2n
main_inner_product = inner_product(l, r)
delta_y_z = (z - z ^ 2) * inner_product(vec_1n, vec_y_n) - z ^ 3 * inner_product(vec_1n, vec_2n)
t = z ^ 2 * v + delta_y_z
assert main_inner_product == t
print("Combined inner product = z ^ 2 * v + delta_y_z.\nWe can continue...\n")
Rescaling the generators: $\mathbf{H'}$
The previous commitments are computed at the very start of the protocol, before receiving any challenge from the verifier.
Therefore, once the verifier sends the challenges $y,z$, we face a subtle issue: $\mathbf{r}$ contains powers of $y$, but $A$ was created before $y$ was known.
Each coordinate of $\mathbf{a}_R$ in the inner product is multiplied by $y^i$, yet the commitment $A$ was made with plain $\mathbf{H}$. We need to reconcile these.
The trick is to absorb the $y^i$ factors into the bases. That’s why we define a new vector:
$$ \mathbf{H'} = \frac{1}{\mathbf{y}^n} \circ \mathbf{H} $$This rescaling ensures that, for any vector $\mathbf{u}$:
$$ \langle \mathbf{y}^n \circ \mathbf{u}, \mathbf{H'} \rangle = \sum_i{(\mathbf{y}^i \cdot \mathbf{u}_i) \cdot (\frac{\mathbf{H}_i}{\mathbf{y}^i})} = \sum_i{\mathbf{u}_i \cdot \mathbf{H}_i} = \langle \mathbf{u}, \mathbf{H} \rangle $$In other words, we can freely “move” the $y^i$ weights from the vector side to the generator side without changing the commitment.
vec_y_n_inv = vec_y_n.apply_map(lambda x: 1/x)
H_y_minus1 = [vec_y_n_inv[i] * Hs[i] for i in range(n)]
Build the point $P$
With this, the prover constructs a single elliptic curve point:
$$ P= \langle \mathbf{l},\mathbf{G} \rangle + \langle \mathbf{r},\mathbf{H'} \rangle $$Using public information, the verifier can express $P$ in terms of the earlier commitments $A,V$:
$$ P \stackrel{?}{=} A - \langle z\mathbf{1}^n, \mathbf{G} \rangle + \langle z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n, \mathbf{H'} \rangle - \alpha \cdot H $$Let me show you this equality explicitly:
$$ \begin{aligned} P &= A - \langle z\mathbf{1}^n, \mathbf{G} \rangle + \langle z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n, \mathbf{H'} \rangle - \alpha \cdot H \\ &= \langle \mathbf{a}_L, \mathbf{G} \rangle + \langle \mathbf{a}_R, \mathbf{H} \rangle + \alpha \cdot H - \langle z\mathbf{1}^n, \mathbf{G} \rangle + \langle z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n, \mathbf{H'} \rangle - \alpha \cdot H \\ &= \langle \mathbf{a}_L, \mathbf{G} \rangle - \langle z\mathbf{1}^n, \mathbf{G} \rangle + \langle \mathbf{a}_R, \mathbf{H} \rangle + \langle z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n, \mathbf{H'} \rangle \\ &= \langle \mathbf{a}_L - z\mathbf{1}^n, \mathbf{G} \rangle + \langle \mathbf{a}_R \circ \mathbf{y}^n, \mathbf{H'} \rangle + \langle z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n, \mathbf{H'} \rangle \\ &= \langle \mathbf{l}, \mathbf{G} \rangle + \langle \mathbf{a}_R \circ \mathbf{y}^n + z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n, \mathbf{H'} \rangle \\ &= \langle \mathbf{l}, \mathbf{G} \rangle + \langle \mathbf{r}, \mathbf{H'} \rangle \end{aligned} $$Perfect! Both representations of $P$ match.
P = A - inner_product(vec_z_1n, Gs) + inner_product(z * vec_y_n + z ^ 2 * vec_2n, H_y_minus1) - blinding_alpha * H
assert P == inner_product(l, Gs) + inner_product(r, H_y_minus1)
Inner Product Argument
Finally the verifier needs to check that $P$ was constructed correctly, based on the values in his possession: $A,V$, the challenges, and the public parameters.
Why does it work? Now that we understand $\mathbf{H'}$, it’s easy:
IPA
Finally, the prover runs an IPA with bases $\mathbf{G}, \mathbf{H'}, Q$ to prove that:
$$ P + t \cdot Q = \langle \mathbf{l},\mathbf{G} \rangle + \langle \mathbf{r},\mathbf{H'} \rangle + t \cdot Q $$where:
- $Q$ is yet another elliptic curve generator chosen by the verifier
- $t = z^2 \cdot v + \delta(y,z)$
The verifier:
-
Reconstructs $P$ from $A,V,y,z$ via the formula above
-
Verifies the IPA proof that $\langle \mathbf{l},\mathbf{r} \rangle = t$
And that’s it! A fully sound but non–zero-knowledge range proof.
print("\nFinally we run the IPA with: P + t * Q")
Q = E.random_point()
ipa_proof = ipa(l, r, Gs, H_y_minus1, t, Q, Fr)
P_full = P + t * Q
verify(Gs, H_y_minus1, P_full, ipa_proof[0], ipa_proof[1], ipa_proof[2], ipa_proof[3], ipa_proof[4], Q, n, Fr)
print("IPA proof ✅")
To check the code for the ipa() function, see here: ipa.sage
And for the full script of our simplified protocol: range-proof-simple.sage
The real Bulletproof adds the missing blinding polynomials to make it private. But structurally, this is already the core of the protocol.
From now on, everything is about privacy… 🙈
Blinding for zero-knowledge: vectors to polynomials
Up to now, we’ve combined our three inner products into one equation, and saw a non-zero-knowledge version of the protocol.
To make the proof zero-knowledge, we need to hide these vectors while still convincing the verifier that the relation holds.
The trick is twofold:
- introduce blinding factors to mask $\mathbf{a}_L,\mathbf{a}_R$
- and move from vectors to polynomials, so we can combine real data and blinding terms in a single structured equation.
Let’s see how the prover builds these blinding polynomials and commits to them using Pedersen commitments, hiding all the secrets while keeping every equation verifiable.
Hiding our vectors with blinding terms
The prover introduces two new random vectors: $\mathbf{s}_L,\mathbf{s}_R$.
They act as noise to mask the real vectors: $\mathbf{a}_L,\mathbf{a}_R$.
Using them, we define two polynomial vectors that depend on a variable $X$:
$$ \begin{aligned} \mathbf{l}(X) &= (\mathbf{a}_L + \mathbf{s}_L \cdot X) - z\mathbf{1}^n \\ \mathbf{r}(X) &= \mathbf{y}^n \circ ((\mathbf{a}_R + \mathbf{s}_R \cdot X) + z\mathbf{1}^n) + z^2 \cdot \mathbf{2}^n \end{aligned} $$When $x=0$, these polynomials reveal the original expression we care about:
$$ \begin{aligned} \mathbf{l}(0) &= \mathbf{a}_L - z\mathbf{1}^n \\ \mathbf{r}(0) &= \mathbf{y}^n \circ (\mathbf{a}_R + z\mathbf{1}^n) + z^2 \cdot \mathbf{2}^n \end{aligned} $$Now look at what happens when we take their inner product:
$$ \begin{aligned} \langle \mathbf{l}(0),\mathbf{r}(0) \rangle &= \langle \mathbf{a}_L - z\mathbf{1}^n,\mathbf{y}^n \circ (\mathbf{a}_R + z\mathbf{1}^n) +z^2 \cdot \mathbf{2}^n \rangle \\ &= z^2 \cdot v + \delta(y,z) \end{aligned} $$This is the core equation we ultimately want to prove.
By turning the vectors into polynomials, the prover can now safely reveal $\mathbf{l}(X),\mathbf{r}(X)$ at one random point (chosen by the verifier) instead of revealing the full secret vectors.
Taking their inner product
What happens when we take the inner product of two polynomial vectors?
If we have: $\mathbf{a}x+\mathbf{b}$ and $\mathbf{c}x+\mathbf{d}$, then:
$$ \langle \mathbf{a}x+\mathbf{b},\mathbf{c}x+\mathbf{d} \rangle = \langle \mathbf{a},\mathbf{c}\rangle x^2 + (\langle \mathbf{a},\mathbf{d}\rangle + \langle \mathbf{b},\mathbf{c}\rangle) x+ \langle \mathbf{b},\mathbf{d}\rangle $$In other words, the result is a quadratic polynomial.
In our case, we call that polynomial $t(X)$:
$$ t(X) = \langle \mathbf{l}(X),\mathbf{r}(X) \rangle = t_0 + t_1 \cdot X + t_2 \cdot X^2 $$The constant term $t_0$ is exactly our target inner product:
$$ \begin{aligned} t_0 &= \langle \mathbf{l}(0),\mathbf{r}(0) \rangle \\ &= \langle \mathbf{a}_L - z\mathbf{1}^n,\mathbf{y}^n \circ (\mathbf{a}_R + z\mathbf{1}^n) +z^2 \cdot \mathbf{2}^n \rangle \\ &= z^2 \cdot v + \delta(y,z) \end{aligned} $$To compute the remaining coefficients $t_1,t_2$ efficiently, we can use a simple Karatsuba trick:
$$ \begin{aligned} t_2 &= \langle \mathbf{s}_L,\mathbf{s}_R \rangle \\ t_1 &= \langle \mathbf{l}(0) + \mathbf{s}_L, \mathbf{r}(0) + \mathbf{s}_R \rangle - t_0 - t_2 \end{aligned} $$This saves some redundant work: instead of expanding everything term by term, we reuse the existing parts to derive the cross-term $t_1$.
So from now on, our goals are:
- Prove that $t_0$ is correct: it equals $z^2 \cdot v + \delta(y,z)$
- Prove that $t(X)$ is well formed:
- $\mathbf{l}(X)$ and $\mathbf{r}(X)$ are constructed correctly
- $t(X) = \langle \mathbf{l}(X),\mathbf{r}(X) \rangle$
Committing to everything
Before the verifier can check anything, the prover must commit to all the relevant values. In a way that’s binding (he can’t change them later) but still hiding (the verifier learns nothing).
These commitments are made to elliptic-curve points and follow a strict order.
We already saw a lot of it when we previously described our “simplified protocol”, but it doesn’t hurt to get a reminder.
Step 1: commit to the secret value $v$
Using a random blinding factor $\gamma$:
$$ V=v \cdot G + \gamma \cdot H $$where $G$ and $H$ are fixed, independent elliptic curve generators.
Step 2: commit to the bit vectors
Now the prover commits to vectors $\mathbf{a}_L$ and $\mathbf{a}_R$, and the blinding vectors $\mathbf{s}_L$ and $\mathbf{s}_R$:
$$ \begin{aligned} A &= \langle \mathbf{a}_L, \mathbf{G} \rangle + \langle \mathbf{a}_R, \mathbf{H} \rangle + \alpha \cdot H \\ S &= \langle \mathbf{s}_L, \mathbf{G} \rangle + \langle \mathbf{s}_R, \mathbf{H} \rangle + \rho \cdot H \end{aligned} $$where:
- $\mathbf{G}$ and $\mathbf{H}$ are vectors of elliptic curve generators (one per bit of $\mathbf{a}_L$)
- and $\alpha,\rho$ are blinding scalars
blinding_alpha = Fr.random_element()
A = inner_product(aL, Gs) + inner_product(aR, Hs) + blinding_alpha * H
print("A = ", A)
# blinding terms for left and right polys
sL = vector([Fr.random_element() for i in range(n)])
sR = vector([Fr.random_element() for i in range(n)])
blinding_beta = Fr.random_element()
S = inner_product(sL, Gs) + inner_product(sR, Hs) + blinding_beta * H
print("S = ", S)
print("\nProver sends A, S, V to Verifier")
Once $A$ and $S$ are committed, the verifier (or the Fiat-Shamir heuristic) can produce challenges $y$ and $z$.
These are then used to define $\mathbf{l}(X),\mathbf{r}(X)$ and $t(X)$.
R.<X> = Fr[]
lX = aL - vec_z_1n + sL * X
print("lX = ", lX)
rX = vec_y_n.pairwise_product(aR + vec_z_1n) + z ^ 2 * vec_2n + vec_y_n.pairwise_product(sR * X)
print("rX = ", rX)
tX = inner_product(lX, rX)
print(f"tX = {tX}\n")
Step 3: commit to $t(X)$
Finally, the prover commits to the coefficients of $t(X)$: the linear and quadratic terms $t_1$ and $t_2$, each with its own blinding factor $\tau_1,\tau_2$:
$$ \begin{aligned} T_1 &= t_1 \cdot G + \tau_1 \cdot H \\ T_2 &= t_2 \cdot G + \tau_2 \cdot H \end{aligned} $$These commitments make sure the prover can’t later tweak $t(X)$ to make the equation magically work.
[t0, t1, t2] = tX.coefficients(sparse=False)
print("Notice that t0 is the inner product we're trying to prove\n")
assert t0 == main_inner_product
blinding_tau1 = Fr(123)
blinding_tau2 = Fr(456)
T1 = t1 * G + blinding_tau1 * H
T2 = t2 * G + blinding_tau2 * H
print("T1 = ", T1)
print("T2 = ", T2)
Putting it all together: verification
Everything is almost ready! 🤩
The prover has committed to all the right pieces. Now the verifier just needs to check that everything lines up.
The final challenge
The verifier sends one last random challenge $x$.
By evaluating the polynomials $\mathbf{l}(x),\mathbf{r}(x)$ and $t(x)$ at this random point, we can check that the claimed relationships hold with overwhelming probability (thanks to the Schwartz–Zippel lemma).
The prover computes:
$$ \begin{aligned} \mathbf{l} &= \mathbf{l}(x) \\ \mathbf{r} &= \mathbf{r}(x) \\ \hat{t} &= \langle \mathbf{l},\mathbf{r} \rangle \\ \tau_x &= \tau_2 \cdot x^2 + \tau_1 \cdot x + z^2 \cdot \gamma \\ \mu &= \alpha + \rho \cdot x \end{aligned} $$Here:
- $\hat{t}$ is the evaluation of $t(X)$ at $x$, equal to the inner product of $\mathbf{l}$ and $\mathbf{r}$
- $\tau_x$ combines all the blinding factors for $t(x)$
- $\mu$ combines the blinding factors for $A$ and $S$
print("\nVerifier sends challenge x\n")
x = Fr.random_element()
print("x = ", x)
# evaluate left and right polys at u
lx = lX(x)
rx = rX(x)
tx = tX(x)
print("lx = ", lx)
print("rx = ", rx)
print("tx = ", tx)
assert tx == lx * rx
print("\nProver sends proof_blindings_mu and proof_blindings_tau to Verifier")
proof_blindings_mu = blinding_alpha + blinding_beta * x
proof_blindings_tau = z ^ 2 * blinding_gamma + blinding_tau1 * x + blinding_tau2 * x ^ 2
Verifier check #1: the polynomial $t(x)$
First, the verifier ensures that $\hat{t}$ matches the claimed polynomial evaluation $t(x)$.
Conceptually, it checks that:
$$ \hat{t} \stackrel{?}{=} \langle \mathbf{l},\mathbf{r} \rangle $$and also that the commitment to $t(x)$ is consistent with all earlier commitments.
The actual check is:
$$ \hat{t} \cdot G + \tau_x \cdot H \stackrel{?}{=} z^2 \cdot V + \delta(y,z) \cdot G + T_1 x + T_2 x^2 $$Why does this hold?
$$ \begin{aligned} t(x) \cdot G &= (t_0+t_1x+t_2x^2) \cdot G \\ t(x) \cdot G &= (z^2 \cdot v + \delta(y,z)) \cdot G + t_1x \cdot G + t_2x^2 \cdot G \\ t(x) \cdot G &= z^2 \cdot v \cdot G + \delta(y,z) \cdot G + x(T_1 - \tau_1 \cdot H) + x^2(T_2 - \tau_2 \cdot H) \\ t(x) \cdot G &= z^2 \cdot v \cdot G + \delta(y,z) \cdot G + T_1x - \tau_1 x \cdot H + T_2 x^2 - \tau_2 x^2 \cdot H \\ t(x) \cdot G + (\tau_1 x + \tau_2 x^2) \cdot H &= z^2 \cdot (V - \gamma \cdot H) + \delta(y,z) \cdot G + T_1x + T_2 x^2 \\ t(x) \cdot G + (\tau_1 x + \tau_2 x^2) \cdot H &= z^2 \cdot V - z^2 \cdot \gamma \cdot H + \delta(y,z) \cdot G + T_1x + T_2 x^2 \\ t(x) \cdot G + (\tau_1 x + \tau_2 x^2+ z^2 \cdot \gamma) \cdot H &= z^2 \cdot V + \delta(y,z) \cdot G + T_1x + T_2 x^2 \\ t(x) \cdot G + \tau_x \cdot H &= z^2 \cdot V + \delta(y,z) \cdot G + T_1x + T_2 x^2 \end{aligned} $$check1_lhs = tx * G + proof_blindings_tau * H
check1_rhs = V * z ^ 2 + delta_y_z * G + T1 * x + T2 * x ^ 2
assert check1_lhs == check1_rhs
print("Check 1 ✅")
Verifier check #2: vectors $\mathbf{l}$ and $\mathbf{r}$
Next, the verifier checks that the revealed vectors $\mathbf{l}$ and $\mathbf{r}$ are consistent with all previous commitments.
We already explained previously what $\mathbf{H'}$ is. But for the lazies, here it is again:
$$ \mathbf{H'} = \frac{1}{\mathbf{y}^n} \circ \mathbf{H} $$Then it computes:
$$ P = A + x \cdot S - \langle z\mathbf{1}^n,\mathbf{G} \rangle + \langle z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n,\mathbf{H'} \rangle $$and checks that:
$$ P \stackrel{?}{=} \langle \mathbf{l},\mathbf{G} \rangle + \langle \mathbf{r},\mathbf{H'} \rangle + \mu \cdot H $$If this equality holds, it means that the prover’s $l(x)$ and $r(x)$ were built correctly.
P = - proof_blindings_mu * H + A + S*x + inner_product(-vec_z_1n, Gs) + inner_product(z * vec_y_n + z ^ 2 * vec_2n, H_y_minus1)
print("P = ", P)
assert P == inner_product(lx, Gs) + inner_product(rx, H_y_minus1)
print("Check 2 ✅")
The Inner Product Argument: the final step
But wait… the prover can’t just send full vectors $\mathbf{l}$ and $\mathbf{r}$, that would reveal too much information.
This is exactly where the Inner Product Argument comes back in!
To prepare for it, we slightly rearrange the equation above:
$$ \begin{aligned} P &= A + x \cdot S - \langle z\mathbf{1}^n,\mathbf{G} \rangle + \langle z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n,\mathbf{H'} \rangle - \mu \cdot H \\ &= \langle \mathbf{l},\mathbf{G} \rangle + \langle \mathbf{r},\mathbf{H'} \rangle \end{aligned} $$and we the inner product result $t$ into it:
$$ P + \hat{t} \cdot Q = \langle \mathbf{l},\mathbf{G} \rangle + \langle \mathbf{r},\mathbf{H'} \rangle + \langle \mathbf{l},\mathbf{r} \rangle \cdot Q $$(where $Q$ is a random elliptic curve point used for the IPA proof).
This is the input to the IPA: the prover produces a short recursive proof that $\langle \mathbf{l},\mathbf{r} \rangle = \hat{t}$.
In case you forgot, you can find our previous articles here: Breaking Down Bulletproofs (part 1) and Unfolding the Bulletproofs Magic (part 2).
Q = E.random_point()
print("Remember that tx = <lx,rx>")
ipa_proof = ipa(lx, rx, Gs, H_y_minus1, tx, Q, Fr)
P_full = P + tx * Q
verify(Gs, H_y_minus1, P_full, ipa_proof[0], ipa_proof[1], ipa_proof[2], ipa_proof[3], ipa_proof[4], Q, n, Fr)
print("IPA proof ✅")
What the final proof looks like
The complete range proof includes:
- $A$ and $S$
- $T_1$ and $T_2$
- $\hat{t}$ and its blinding factor $\tau_x$
- $\mu$ (blinding for $A$ and $S$)
- the IPA proof, which consists of:
- $L$ and $R$ vectors, from each folding step
- two scalars representing the final folded vectors $\mathbf{l}$ and $\mathbf{r}$
And that’s it! we’ve just built a complete range proof from the ground up! 🧠
Starting from a simple idea: proving that a hidden value lies between 0 and $2^n$, we combined a series of powerful tricks:
- Bit decomposition to express the value as a vector of 0s and 1s
- Random challenges ($x,y,z$) to tie every equation together and prevent cheating
- Commitments to hide the data while keeping all relationships consistent
- Blinding of inputs and outputs of IPA, as the IPA protocol is not zero-knowledge
- And finally, the Inner Product Argument to verify everything efficiently and compactly
All of that comes together so that a verifier can be convinced that: “the prover’s secret value lies in the correct range”, without learning anything about the value itself.
This foundation powers confidential transfers, private balances, and many other privacy-preserving systems, like the one we sketched at the start of this article.
You can find the entire Sagemath script here: range-proof.sage