Bitcoin has long been considered limited in its ability to verify arbitrary computations (including verifying zero-knowledge proofs!). However, recent developments of BitVM variants have shown the potential to verify arbitrary computations on Bitcoin without modifying its core protocol.

The BitVM1, which is formalized in an eprint paper, introduced the circuitry idea to enable arbitrary computation on Bitcoin. It employs an optimistic protocol where computations can be done off-chain, and resolved on-chain among the roles of proposer and challenger when there is a dispute over the computations. However, it has fixed verifiers, meaning only predefined parties can challenge claims.

Building on this concept, the BitVM2 paper introduces a bridge protocol that allows cross-chain asset verification, such as transferring assets between Bitcoin and other blockchains with minimal trust. It generalizes the process by compressing and verifying computations via a SNARK verifier encoded in Bitcoin scripts.

BitVMX is another variant of BitVM1, but aims to be less complex and an efficient alternative to the BitVM2.

In this post, we explore the fundamentals of Bitcoin’s Unspent Transaction Output (UTXO) programming model and examine how the building blocks introduced in the BitVM1 overcome the inherent limitations to enable arbitrary computation. With this background, we hope the post paves the way for a deeper understanding of similar BitVM systems.

Understanding Bitcoin’s UTXO Model

Ethereum uses an account-based programming model, where transactions update the global state of accounts. Each block records the effects of state transitions, and subsequent transactions further modify these account states. This aligns well with traditional programming models, where a program maintains and updates its state over time.

In contrast, Bitcoin’s UTXO (Unspent Transaction Output) model is more restrictive. Each Bitcoin transaction “spends” existing UTXOs and creates new ones. Spending a UTXO involves executing a locking script (part of the UTXO) with a corresponding unlocking script (the transaction witness data). These scripts are stateless: once a UTXO is spent, there is no update to global state aside from creation of new UTXOs.

A Bitcoin transaction consists of the following:

• Inputs: UTXOs to be spent
• Outputs: newly created UTXOs
• Witnesses: Data that unlocks the inputs

When spending a UTXO, the witness data in the transaction must satisfy its locking script. Additionally, the total value of BTC in the inputs must exceed that in the outputs, with the difference serving as the transaction fee.

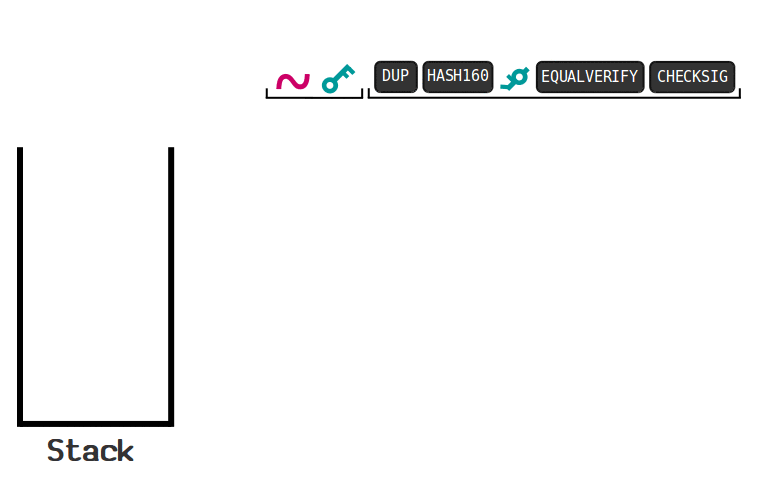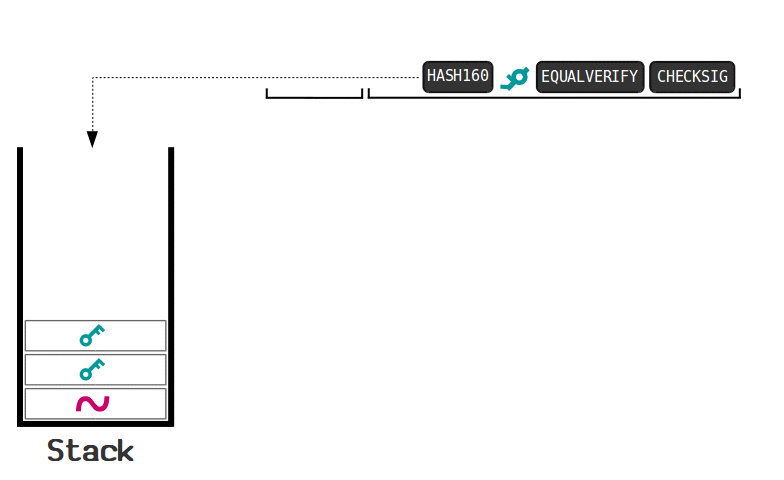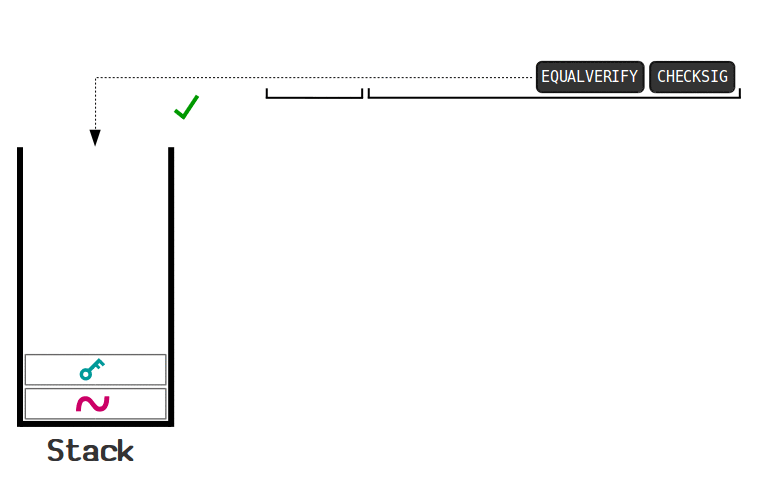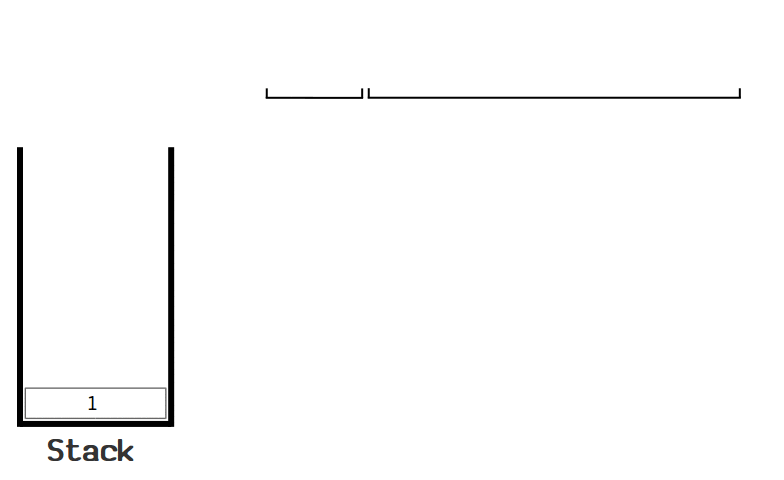
The following animation demonstrates how a UTXO locked by a “signature required” script is unlocked:

source: https://learnmeabitcoin.com/

Bitcoin Script is a stack-based language. Following the FIFO (First In, First Out) order, the script executes the opcodes and pushes the results onto the stack. Execution is considered valid if the only remaining element on the stack is the value 1; otherwise, it is deemed invalid.

The execution serves as a verification process. A UTXO can only be spent when the provided witnesses successfully pass the execution of the locking script.

In theory, the locking script language can encode an arbitrary program. However, it does not support features such as loops or provide access to external memory storage. Furthermore, the maximum size of scripts is constrained by the 4 MB block size limit. These limitations render large, complex scripts impractical.

Building Circuit Abstractions on Bitcoin

A natural question arises: How can we circumvent the limitations while still enabling complex program logic?

One approach is to divide a larger program into multiple UTXOs, each encoding a small subset of instructions (often referred to as “circuit gadgets”). Transactions then function as the “wires” connecting these gadgets. Executing the entire program involves creating a series of transactions that together implement the desired logic.

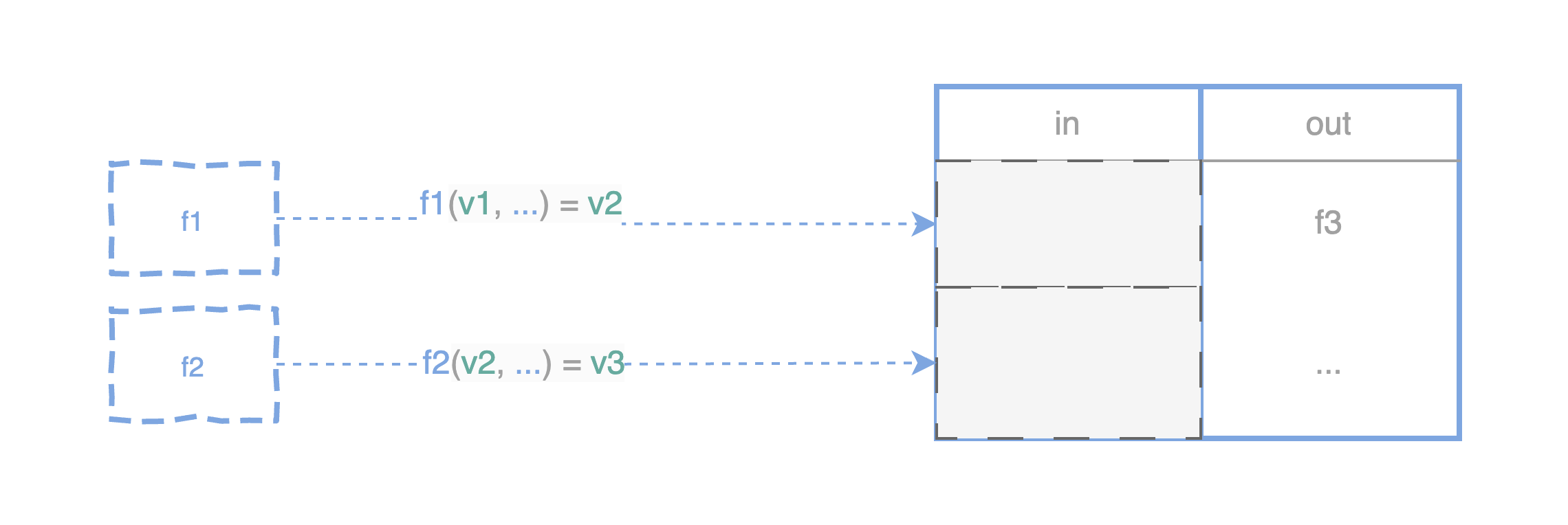
Consider a program consisting of the following executions:

f1(v1) = v2
f2(v2) = v3
f3(v3) = v4

By decomposing it into smaller locking scripts, we can form a circuit that achieves the same state transitions as the entire program. This approach circumvents the script size limit.

The diagram below illustrates this concept:

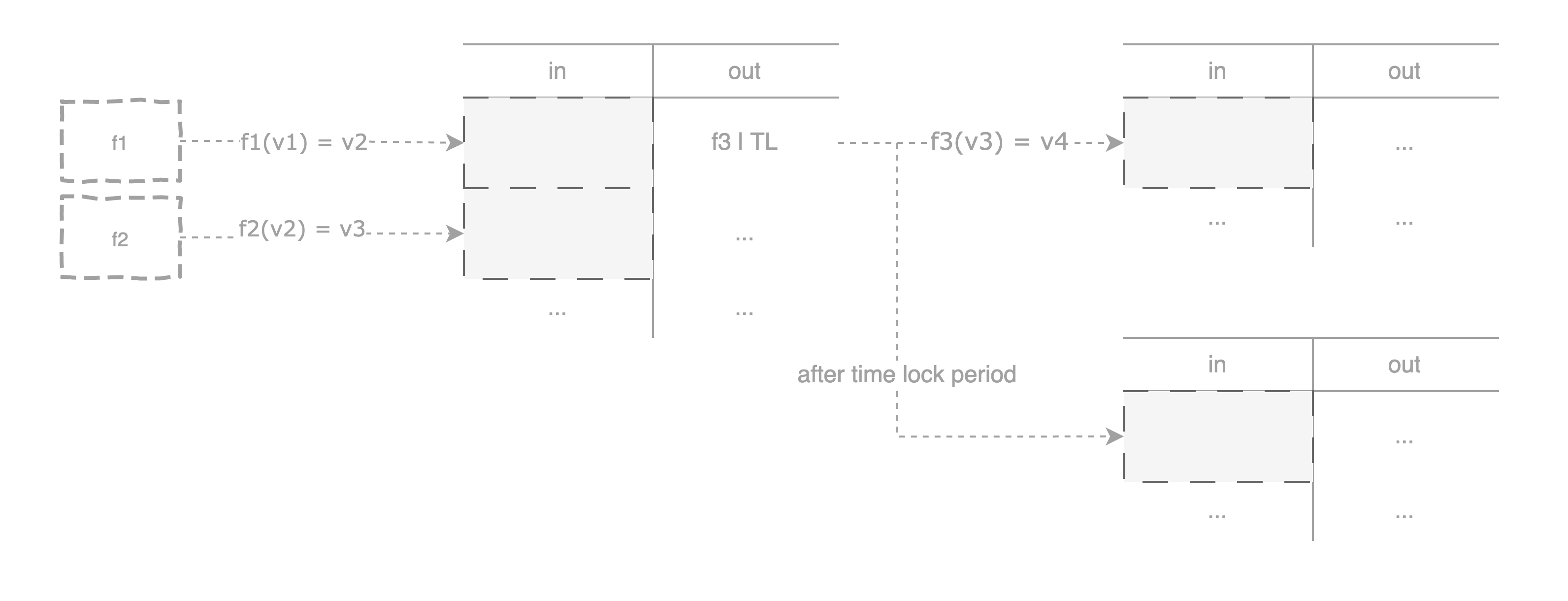
• On the left, the UTXO with the f1 locking scripts can be unlocked if correct arguments v1 and v2 are provided. It represents a partial verification of program execution, serving a similar role to gates or gadgets in a circuit.
• A transaction can unlock multiple UTXOs by providing witnesses that satisfy the locking scripts, such that validate f1(v1)=v2 and f2(v2)=v3 concurrently, and create new UTXOs for the next state transitions. This is akin to wiring between the gadgets in a circuit.
• On the right, a UTXO can be spent via different paths, such as unlocked by f3(v3)=v4 or time lock script TL. This resembles a branching in a circuit.

However, we cannot directly use the Bitcoin script to implement such a circuit abstraction on top of the Bitcoin UTXO model. This is due to two main issues:

• Locking scripts are self-contained. While a locking script can force a state transition to be correct (e.g. f1(z1) = v2) we cannot force the transaction that spends it to create a new UTXO enforcing the continuation of our circuit (e.g. a f3 locking script in the produced UTXOs, forcing the circuit to continue its evaluation instead of unlocking the funds directly).

• Locking scripts are stateless. Even if we could enforce a certain “circuitry”, another problem is that the state is contained in the witness (or unlocking script) and as such cannot be “passed around” between UTXOs. In essence, Bitcoin scripts are stateless and do not allow passing data between them. For example, we cannot enforce that the witness v2 produced by f1 is the same as the witness v2 used by f2, as f1 and f2 are in different locking scripts / UTXOs. Another example is that the witness unlocking f3 can’t be forced to use the same v3 that was witnessed in the preceding transaction

Next, let’s see how the BitVM line of work addresses each of these challenges.

Overcoming UTXO Limitations: Wires & Signal Constraints

These challenges can be addressed by incorporating two key building blocks: emulated covenants and statefulness via one-time signatures.

Emulated Covenants with Multi-Signature Setup

Covenants are a Bitcoin concept that constrains how a UTXO can be spent. They are similar to the wires in a circuit, dictating how signals flow between gadgets.

A locking script defines the requirements (witnesses) needed to unlock a UTXO. However, it doesn’t know about the overall transaction structure in which the UTXO is used. To ensure this proper placement and interaction in subsequent transactions, we need a way to restrict how a UTXO can be reused. This restriction is achieved through covenants.

As of this writing, Bitcoin doesn’t yet support native covenants features. There are ongoing efforts in the Bitcoin community to support native covenant features. One of them is the OP_CHECKTEMPLATEVERIFY (CTV) opcode. These opcodes enable the locking script of a UTXO to validate the transaction template, though they require a hard fork. Other innovative approaches include ColliderScript from StarkWare, and Un-FE’d Covenants, etc.

The BitVM paper proposes an emulated covenants solution using multisig to constrain the future spending rules for the UTXOs by pre-signing transactions. In this post, we explain the concept of emulated covenants.

How Multisig Works

A locking script with multisig allows a UTXO to be spent only when a predefined number of parties agree, often referred to as a threshold. Unlike typical transactions requiring just one signature, the script can specify how many signatures are required from a set of public keys. The exact number of signatures required is specified by opcodes such as OP_1, OP_2, etc., with the overall validation performed by OP_CHECKMULTISIG.

Multisig requirements are commonly expressed as “M-of-N,” meaning that M signatures from a total of N provided public keys are necessary to authorize spending. For example, a “1-of-2” multisig setup requires a signature from any one of two specified public keys:

OP_1                      # Require at least 1 signature (M=1)
<PUBKEY_A> <PUBKEY_B>     # Two possible public keys
OP_2                      # Total number of public keys (N=2)
OP_CHECKMULTISIG          # Checks if at least one signature matches the provided keys

On the other hand, an “N-of-N” multisig (e.g., 2-of-2 or 3-of-3) requires signatures from all specified public keys, ensuring consent among all participants.

Since multisig requirements are specified directly within the locking script, they can form part of more intricate logic for spending conditions.

Locking Transaction Templates Using Sighash

A sighash type defines the structure of a transaction that a signature should be bound to. By specifying a sighash type, signers can bind their signatures to particular transaction elements, such as the arrangement of inputs and outputs.

The common sighash type, SIGHASH_ALL, invalidates the signature if any part of the transaction is altered. When combined with multisig, signatures can collectively enforce agreement on a transaction template. Thus, a participant can’t modify the agreed template without invaliding the signatures.

By enforcing requirements on the UTXOs these transactions can produce, one can enforce a path for the entire subtree of possible transactions that can arise from spending the original UTXO.

Emulating Covenants with Multisig

Covenants allow us to shape the trajectory taken by a UTXO, by encoding how transactions that wish to spend that UTXO must look like. Take the locking script f1 for example. By extending the script f1(v1)=v2 with multisig conditions, participants can ensure transactions adhere strictly to agreed-upon templates. This setup leverages multisig signatures to bind transaction structures and enforce covenant-like restrictions on UTXOs:

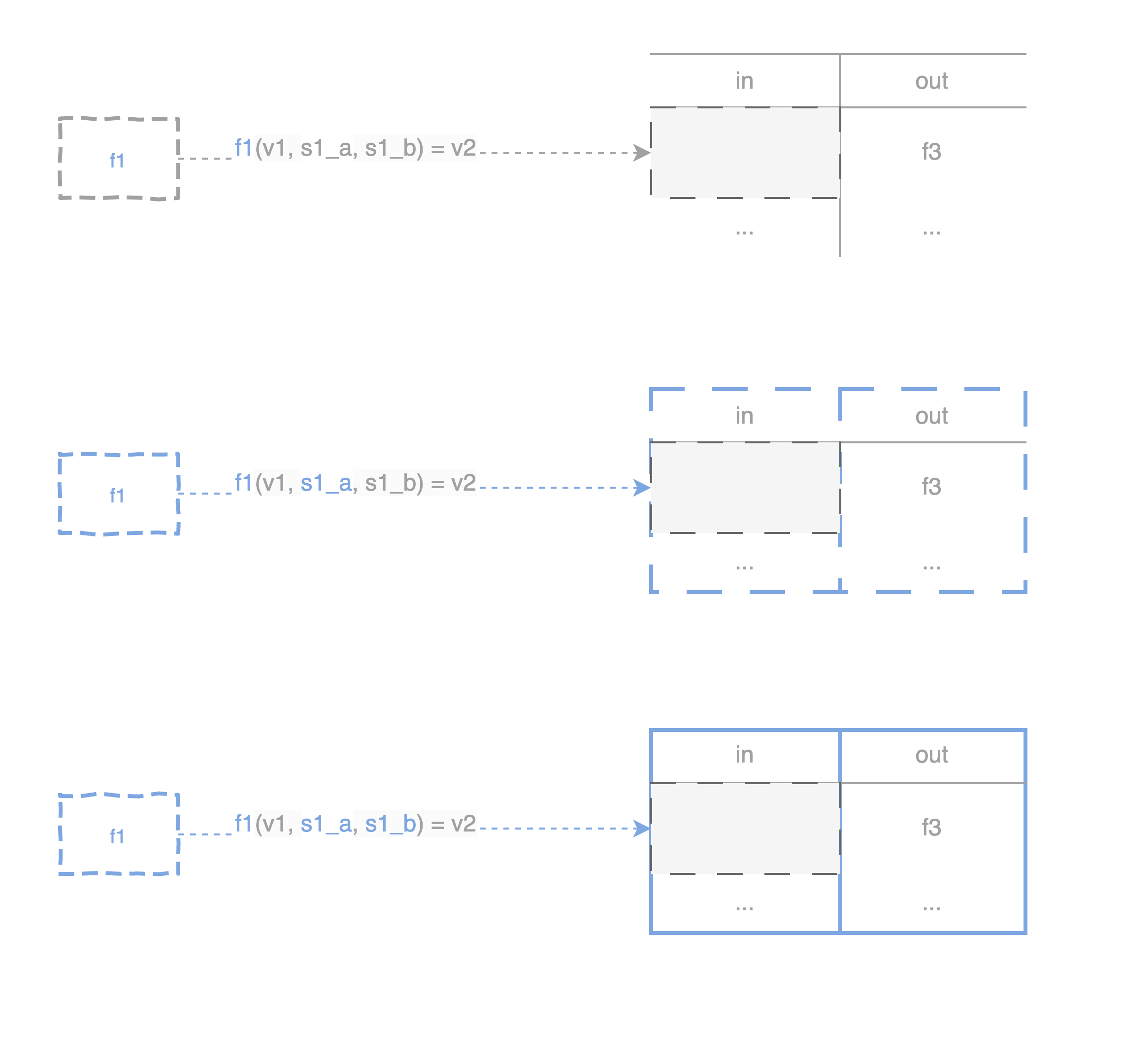
• Party A provides a partial signature s1_a, binding the transaction specifically to an input UTXO with locking script f1 and an output UTXO with locking script f3.

• Party B similarly provides another partial signature s1_b, binding the same transaction structure.

• Both signatures combine to form a pre-signed transaction template, ensuring consistency in the UTXO flow.

By applying this approach recursively, each newly created UTXO (such as those with locking script f3) can be similarly controlled, creating a chain or graph of pre-signed transaction templates. This chaining mechanism ensures that transactions strictly adhere to agreed conditions, effectively forming a skeleton of the “user circuit” over the UTXO model.

Note that these pre-signed transactions only become complete when additional arguments (like v1, v2 for a transaction) are supplied, which are we are going to fill the skeleton with. These arguments represent the circuit signals. This statefulness aspect will be detailed in subsequent sections.

Enforcing Static Single Assignment with One-Time Signatures

With the covenants in place, the pre-signed transactions can be published on-chain in order by providing the variable witnesses such as v1 and v2 for locking script f1 along with the pre-filled multisig signatures.

The problem is that the locking script is stateless. It can’t constrain the consistency in the arguments, such as v1 and v2, across different UTXOs:

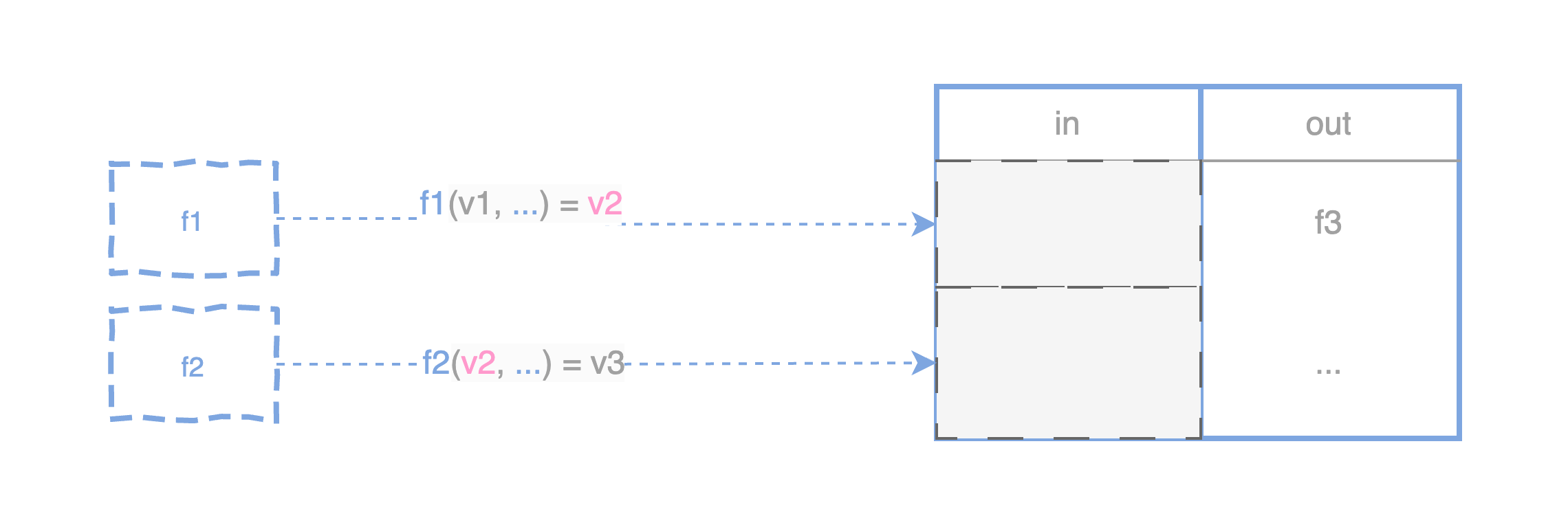
For example, without enforcing the immutability of the locking script arguments, the argument v2 can be assigned two different values across different locking scripts. This doesn’t guarantee state transitions represented by the f1 and f2 locking scripts, as it can make up different values for v2 to just pass the execution of a locking script.

To enforce immutability of variables, the BitVM line of work makes use of one-time signatures in conjunction with a slashing protocol. This trick was originally proposed in 2021 in here. One-time signatures are signature schemes that can only be used once. While this is quite limiting, they have the particularity that one can easily detect if they are used twice to sign different values. As such, we can create one one-time public key for each variable we have, and use their associated one-time signature on the value we assign the variable to.

In fact, this approach closely resembles the static single assignment SSA model used in compiler design. By enforcing a single assignment per variable, the system can achieve predictable and verifiable state transitions.

source: https://en.wikipedia.org/wiki/Static_single-assignment_form

How Lamport Signature Works

Before diving into the details of how it achieves statefulness in our circuit model, let’s review how Lamport signature scheme.

The table below illustrates the relationship between a Lamport signature’s public key, private key and the 1-bit to sign.

The public key is a pair of hashes H(x), H(y).

To sign the message, reveal the signature (private key) x or y based on its corresponding bit value 0 or 1.

To verify, the signature can be hashed using function H to check if it matches with the corresponding hash in the public key.

Similarly, for an n-bit message, there will be n pairs of private keys. Suppose it is for a 256 bit message, there should be 256 pairs:

Emulating Statefulness with Lamport Signature

The way to set up the Lamport signature depends on the protocol. The setup phase of Lamport signature involves preparing both the public key and private keys. In the circuit model over the UTXO model, these private keys should be only known to the participants who generate the public keys for variables. For simplicity in this post, we assume the protocol is based on proposer-challenger model, in which the proposer sets up the Lamport signature and commits to the variable values while the challenger is incentivized to detect and prove equivocations.

In the above diagram, the arguments in green color, such as v1 and v2, representing stateful variables to unlock the f1 are tuples. Each tuple comprises of (val, sig), representing the variable value and signature (private key) - the commitment to a variable value. By applying with the Lamport signature scheme, the locking script can verify the commitment against the public key hardcoded for a variable:

Now it comes with the most critical part of using one-time signatures like Lamport signature for the commitment enforcement in order to emulate statefulness: Equivocation. Without a way to detect and punish equivocation, there are no enforcements for the proposer to commit to the correct variable values.

The idea of proving equivocation is relatively simple. As long as the challenger finds the proposer equivocates a variable value, at least a full pair of signatures for the variable value must be revealed. The challenger can publish the equivocation transaction with the full pair of signatures for a variable, such as $(x_1, y_1)$, to prove the proposer equivocates the variable value:

In terms of how to punish the equivocation, it is up to the actual protocol. Presumably, the covenants should also include a set of pre-signed transactions that can be used to prove an equivocation over each variable in the circuit model.

Time Lock as an Intra-Script Branching

Certain protocols, such as optimistic protocols, rely heavily on interactions between participants to advance their states. During each interaction round, participants are expected to respond promptly. To prevent a participant from halting or stalling the protocol, time lock scripts can enforce strict response deadlines by serving as an alternative spending path:

OP_IF
    <default spending condition (e.g., multisig)>
OP_ELSE
    <future timestamp or block height> OP_CHECKLOCKTIMEVERIFY OP_DROP
    <alternate spending condition (e.g., signature from the other side)>
OP_ENDIF

In this example, the other side of participant(s) on the other side can spend the UTXO after the time lock period if the default spending condition is not met. This intra-script branching ensures that the protocol can advance even if one participant becomes unresponsive.

Extra-Script Branching among Pre-Signed Transactions

While intra-script branching handles conditional logic within a single locking script, extra-script branching invalidates certain paths within a transaction graph after a UTXO is spent. A common pattern used for extra-script branching is Connector Output, a technique described in the BitVM bridge paper

In computational circuits, states follow conditional branches leading to distinct outcomes. Similarly, Connector Outputs allow a UTXO to be consumed by exactly one pre-signed transaction, automatically invalidating alternative pre-signed transactions. This ensures mutual exclusivity in transaction pathways, mirroring conditional branching found in circuit logic.

Compress Large Scripts with Taproot

Bitcoin scripts have inherent size limitations due to block size constraints, restricting the complexity of logic that can be directly embedded within individual UTXOs. Taproot can address this limitation by enabling multiple scripts to be compressed into a single, compact Taproot output.

The original BitVM1 paper illustrates the idea of allowing circuit gates to be represented as commitments because it encodes multiple spending conditions (scripts) into a compact Merkle tree structure. Each circuit gate, represented as an individual spending condition (Tapleaf), is hashed and included as a leaf in the Merkle tree. The root hash of this Merkle tree is committed to within the Taproot output.

This allows complex transaction logic, or even entire computational circuits, to be encapsulated within a single UTXO. Instead of embedding extensive locking scripts explicitly, Taproot aggregates these scripts into a script commitment, revealing each script only as needed at spending time. It is particularly useful for achieving more flexible extra-script branching, where Taproot allows a Connector Output to carry much more intra-script branches.

User Circuit Compilation and Execution

Leveraging the previously described building blocks, we can effectively “compile” and “execute” user-defined computational circuits over the UTXO model. The core components for this approach include:

• Covenants: Ensuring agreement on the transaction graph representing the user circuit.

• One-time signatures: Enforcing single assignment for variables, analogous to the static single assignment (SSA) concept in compiler design.

• Intra-script and extra-script branching: Emulating complex conditional logic necessary for executing intricate circuit designs.

By combining these elements, a user-defined computational circuit can be systematically compiled into a UTXO-based representation and executed in a deterministic manner.

An example workflow for the proposer-challenge model is as follows:

1. Encoding Variables: The proposer generates a unique public-private key pair for each variable in the circuit. Public keys for these variables are hardcoded directly into the locking scripts, effectively encoding circuit variables into UTXOs.

2. Pre-signing Transactions (Proposer): The proposer creates the raw transactions withese encoded variables, and pre-signs them with multisig for covenants.

3. Pre-signing Transactions (Challenger): The challenger reviews and pre-signs the transactions for the covenants, verifying that the public keys accurately encode variables consistently across different UTXOs. At this stage, the user circuit is compiled over the UTXO model.

4. Executing the Circuit: To advance the circuit’s state, the proposer publishes transactions containing commitments to variable values. These commitments unlock the corresponding UTXOs using the previously agreed-upon pre-signed multisig transactions, thus executing the circuit and pushing its state forward.

Protocol Overview to Offload Computation

With the building blocks described in the previous sections, we are now ready to tackle the optimization problem. It is easy to see that directly modeling a large program as a circuit and publishing the entire circuit on-chain would be too slow and economically infeasible.

There are ways to address this issue. BitVM1 proposes an optimistic protocol that incentivizes honest commitments to the data on-chain and punishes equivocation through a bisection game to locate the error. On the other hand, BitVM2 also proposes an optimistic protocol but does so more efficiently by compressing the program using SNARK.

To understand how to make the circuit model described above feasible, here is an overview of the optimistic protocol with a bisection game to keep the on-chain footprint small while ensuring the proposed computation is correct:

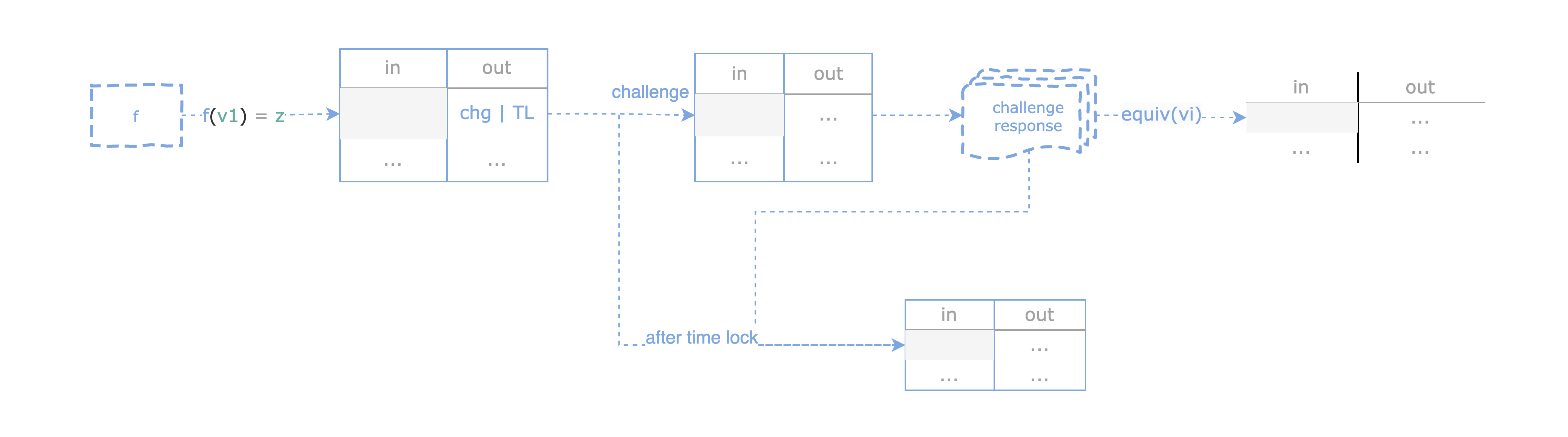
1. There are two parties: the proposer and the challenger.
2. Both parties pre-sign the covenants.
3. Proposer publishes a transaction with commitments to input v1 and output z of the locking script f representing the execution of the entire program.
4. The newly created UTXO can be either consumed by the dispute transaction by the challenger, or by the proposer after the time lock period.
5. In the event of a dispute, the participants respond to each other in turn in a bisection game to locate the error within a fixed number of rounds.
6. Once the error is found, the challenger can publish an equivocation transaction to consume the UTXOs, which contain the deposits from the proposer, as a penalty.
7. During the dispute period, either party can consume the UTXO if the other party fails to respond after the time lock period.

In a future post, we may explore these optimistic protocols in more detail to reveal how they leverage the circuit model.

Conclusion

By layering a circuit model over Bitcoin’s UTXO programming paradigm, through the building blocks, such as emulating covenants, statefulness and branching, etc. — an user circuit can be modeled into a UTXO circuit. To make this approach practical, optimistic protocols such as those proposed in the BitVM papers can enhance on-chain efficiency by keeping the on-chain footprint minimum. Together, these techniques not only expand Bitcoin’s capabilities without altering its core protocol but also pave the way for the efficient verification of arbitrary computations.